3 模型理论分析

    假设新感染节点加入蠕虫网络前网络中节点总数为n，那么网络中任意一节点i 被选为游走起始节点的概率P(i)=1/n 。若节点j 是节点i 的一个邻居，以P(j)表示游走到达节点j 的概率。根据贝叶斯规则 

 
(1)

式(1)中条件概率P(j\i) 表示随机游走者以节点i 作为游走起始节点后，随机游走到邻居节点j 的概率，可表示为 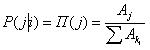  ( A_j为节点j 当前的吸引力，k_i表示节点i 的邻居数)，而∑A_ki可以进一步表示为k_i <A_ki>（<A_ki>为节点i 的邻居节点具有的平均吸引力），同理可得P(j\i) 可以表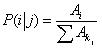示为  ， 可以表示为  ，将相关结果代入式(1)可得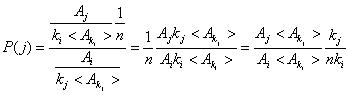
 (2)
式(2)中,  ，若令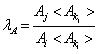  ，则式(2)可以表示为  。
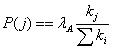    从蠕虫网络演化过程易发现，每个时步有一个新节点加入网络，因此蠕虫网络是一个动态增长的过程。下面借助平均场理论^[5]来分析节点度分布的规律。假设节点i在第i时步加入网络, 初始节点两两连接，则t 时步网络中各节点度数总和  ，变量k_i(t)对应于t 的变化率可表示为
 (3)
在一个长时间的演化过程里，有  ，则式(3)可转化为：
 (4)
新节点加入网络时都要建立m 个连接，则式(4)有初始条件k_i(t_i)=m 。解微分方程(4)，得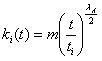
 (5)
求得i时步加入的节点在t时刻的度数。设新感染节点在相同时间间隔内被连接到网络中，那么t_i 的概率密度函数为f(t_i)=1/(m₀+t) ，根据节点度分布P(k,t) 的定义，有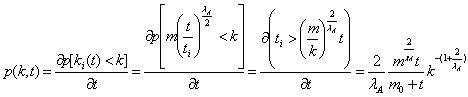
 (6)
    而在实际的蠕虫传播过程中, 用户的对抗措施可能使一些蠕虫节点脱离蠕虫网络。在根据节点吸引力采用随机游走的方法构建网络的过程中，如果发现邻居已经脱离蠕虫网络，可以重新选择游走方向，吸引力高的节点将被优先选择，蠕虫网络的构建能够正常进行。

4仿真与讨论

    为了进一步证实前面的计算结果，对传播模型作计算机模拟。假设蠕虫网络服从增长的模式，即每隔一个时间单元，都有一个新的感染节点加入网络，初始网络有5个节点，相互连接，为了仿真简单取  。新加入的节点依据吸引力优先的原则和网络中的3个节点相连。经过5000时步后计算节点度的分布，整个过程重复20次，取统计平均值。仿真结果如图1(a)所示, 结果表明模拟值与理论值吻合得比较好，且与Barabasi ^[3]模型类似

(责任编辑：adminadmin2008)