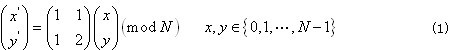(1 中南民族大学 计算机科学学院 武汉 430073 2中国软件评测中心(CSTC) 北京 100048)
摘要:文中提出一种基于小波的二值图像盲数字算法,首先引出小波变换理论的小波变换域的方法,以保证水印的不可见性和鲁棒性,并进行Arnold变换来对抗几何攻击,试验表明,这种水印算法是具有较强的安全性,并能保证二值图像质量有较强的鲁棒性。
关键词:二值图像;数字水印;小波变换;Arnold变换
The Digital Binary Image Blindly Watermarking Algorithm Based on Wavelet
1JIANG Tian-fa, 1WANG Li, 2JIANG Wei, 1XIONG Xiang-Guang
(1 College of Computer, S. Cent. Univ. Nationalities, Wuhan 430073 2 China Software Test Center ,Beijing 100048)
Abstract:This paper presents a new digital binary image blindly watermarking algorithm based on wavelet.First,it introduces the wavelet transform domain method to increase the unobtrusiveness and robustness.Second,it uses the Arnold transform to against the geometric attacks.Experimental results show the proposed algorithm has strong security and very robust to common brinary image guality.
Keywords: binary image;digital watermarking;wavelet transform domain; Arnold transform
1引言
由于二值图像的特点,对图像的随意修改将可能造成图像的严重失真,另外,二值图像数字水印算法的一个重要特点就是水印的鲁棒性和嵌入容量是相互制约的,如果要增强鲁棒性,就必须要将水印信息嵌入在合理的位置上,不能将其嵌入在某些特定的位置上,即必然以牺牲嵌入容量作为代价[1,2]。针对这些问题,本文提出了一种基于小波的二值图像盲水印算法。该算法首先对水印图像首先进行置乱,将水印变成看似杂乱无章的信号,这一方面可以防止对水印系统的攻击,增强系统的安全性,另一方面,使含水印图像部分被破坏时可以尽可能的分散错误比特。其次在水印嵌入过程中采取了基于小波变换域的方法,很好的保证了水印的不可见性和鲁棒性。并且在提取水印的过程中不需要原始图像,实现了盲水印功能。
2 小波域图像水印算法
基于小波变换的图像水印方法相对于DCT(Discrete Cosine Transform,离散余弦变换)和DFT(Discrete Fourier Transform,离散傅立叶变换)有许多独特的、适合于图像水印的特性[1,3]。小波变换的时频局部化特性为分析图像的局部特征提供了很好的定位,这些局部特性往往可以通过不同分辨率下对应的系数推导出来,从而可以利用小波系数的局部特性来嵌入水印。基于小波变换的图像水印方法也很容易与HVS(Human Visual System,人类视觉系统)相适应。人眼对不同空间频率、不同方向上的敏感度是不同的,一般对低频变化的敏感度高于高频,对水平方向和垂直方向的敏感度高于对角线方向,而小波分解正是把图像分解成不同空间分辨率、频率特性和方向特性的子图像。因此,可以根据人类视觉掩蔽特性设计不同的水印嵌入方式,以提高水印在视觉上的不可感知性和抗攻击能力。
在小波域图像水印算法中,有多种小波基可供选择,可以根据具体的应用选择最适合的小波基。图像的小波分解级数也可以根据需要来选择,这些选择都和密钥一样是保密的,有利于提高算法的安全性。
小波域水印也和其他域的水印技术一样分为水印添加、提取(检测)两部分。小波基的类型、水印的选取、水印嵌入的强度和水印嵌入位置都会影响到水印系统的性能,包括水印的不可见性和鲁棒性。
在小波域嵌入和提取水印中,小波基的选择、边界处理、小波分解级数和小波系数的量化等因素都影响数字图像处理的效果。小波分解的级数越多,产生的子带越多,对频带的划分越细,有利于编码和图像处理,但级数的增加意味着滤波器的级联次数越多,造成的信号移位也越大;另一方面,由于每次分解都要进行边界延拓,级数愈多引起的边界失真也越大,所花费的时间也越多[4]。因此在实际应用中,确定小波分解的级数要兼顾不同方面的影响。
3 小波基、分解级数及小波系数的选择
设计小波域水印算法一个很重要的问题是小波基的选择,基于不同小波基的水印鲁棒性不同。小波分正交和双正交两类都适用于水印算法。
已有研究表明[5],正交小波基的正则性、消失矩阶数、支撑长度以及小波图像能量在低频带的集中程度对水印鲁棒性影响极小。在Daubechies小波中,Haar小波在数字水印的算法中体现出了优良的性能[6],而且Haar小波的支撑长度最短,分解和重构计算复杂度低于其它小波。同时Mallat算法是针对无限信号的,而实际中的图像是有限的需要延拓,而对Haar小波而言边界不需要延拓。因此本算法采用了Haar小波基。
小波分解是每级以2加权,并且低通滤波器系数和为1,从而随着小波分解级数的增加,低频系数的幅值以近似2的倍数增长。而水印的嵌入可以看作是在强背景(原始图像)下叠加了一个弱信号(水印),只要叠加的信号低于对比度门限,视觉系统就无法感觉到信号的存在。根据Weber定律[7],对比度门限与背景信号的幅值成比例,因此随着小波分解级数的增加,嵌入水印的强度就可以以近似2的倍数增加,从而可以增加水印的鲁棒性,同时水印信号也能更好的扩散。因此在水印算法中,应根据原始图像的大小和水印数据量的多少,尽可能提高小波分解的级数,但也要同时考虑小波分解和重构需要的时间长短。本算法中,原始二值图像大小为256×256,水印二值图像大小为32×32,小波分解级数为2。
4 水印的生成
4.1 水印的选择
水印的选择通常有两种:一种是向专门的版权保护部门登记并申请得到一个版权ID号,该版权ID号是一个有足够长度的数字码,并保证该ID号在全世界是唯一的。另外一种是采用一幅小的有意义的图像,该图像的内容表明原始图像的版权信息。与前者相比,采用一幅有意义的图像作为水印信号具有很好的鲁棒性,由于图像的可见性,可以很直观的检测是否含有水印。另外,由于人眼的分辨率有限,即使出现多个比特错误也不会影响水印的识别。所以本文嵌入的水印信号是一幅32×32的有意义的二值图像。
4.2 水印的置乱预处理
如果将水印直接嵌入到图像当中,当攻击者从载体数据中获得了水印数据,就可以了解水印内容,对水印的攻击就会变得非常容易,所以本文在将水印嵌入到图像之前首先进行置乱预处理。所谓置乱,就是运用一定的规则搅乱图像中像素的位置或颜色,使之变成一幅杂乱无章的图像,达到无法辨认出原图像的目的[8]。在水印图像的预处理中,可以通过置乱去除水印图像像素间的相关性,分散错误比特的分布,使水印呈现出类似白噪声的特性,从而提高水印系统的鲁棒性。
在图像加密中,置乱技术主要关心的是加密强度或解密难度。而在水印技术中,重点考虑的是置乱效果以及置乱时间和复原时间的开销。目前,人们用的比较多的置乱技术有Arnold变换、幻方变换、分形Hilbert曲线、Gray码变换、混沌序列等方法[9]。其中,Arnold变换算法简单且置乱效果显著,在数字水印方面得到了很好的应用。
Arnold变换(Cat mapping)是Arnold在遍历理论的研究中提出的一种变换,俗称猫脸变换,是一种传统的混沌系统,其定义如下[10,11]:
其中,(x,y)是像素在原图像的坐标,(x',y')是变换后该像素在新图像的坐标,N是数字图像矩阵的阶数,即图像的大小,一般考虑正方形图像即矩阵。
当对一个图像进行Arnold变换时,就是把图像的像素点位置按公式(1)进行移动,得到一个相对原图像混乱的图像。对一幅图像进行一次Arnold变换,就相当于对该图像进行了一次置乱,通常这一过程需要反复迭代多次才能达到满意的效果。
利用Arnold变换对图像进行置乱使有意义的数字图像变成像白噪声一样的无意义图像,实现了信息的初步隐藏,并且置乱次数可以为水印系统提供密钥,从而增强系统的安全性和保密性。
Arnold变换可以看作是裁剪和拼接的过程,通过这一过程将数字图像矩阵中的像素重新排列,达到置乱的目的。由于离散数字图像是有限点集,对图像反复进行Arnold变换,迭代到一定步数时,必然会恢复原图,即Arnold变换具有周期性。F.J.Dyson和H.Falk给出了对于任意N>2,Arnold变换的周期![]() 的结论,这虽然是比较粗略的估计,但也许是迄今为止最好的结果。
的结论,这虽然是比较粗略的估计,但也许是迄今为止最好的结果。
(责任编辑:adminadmin2008)